どうも「針たむ」です。
今まで48年間生きてきましたが、これほどの衝撃はありませんでした。
今までこれほどまで、頭の中に保存してあった常識が思い切り覆された事があったでしょうか。
今どきの子たちは知っているのかも知れないけれど、これはまさに「目から鱗」の手法ですね。
線と点を用いた計算方法というのがある

インド式計算という言葉は聞いたことがある。
しかし、似たような原理であろうと思える「線と点を使った計算方法」というのを恥ずかしながら今日、知ることになった。
きっかけはFB(フェイスブック)の動画を観ていた時だ。
何だこれ?的な思いで、別に気にもしないで閲覧していたところ今までに見たこともない方法で計算を解いているではないか。
かなり興味を惹かれたので、知らない人のために以下に詳細を書いていきます。
計算の方法
計算の順序的にはこうだ
- 数字に応じた線を引く
例として123☓321という計算をしてみましょう。
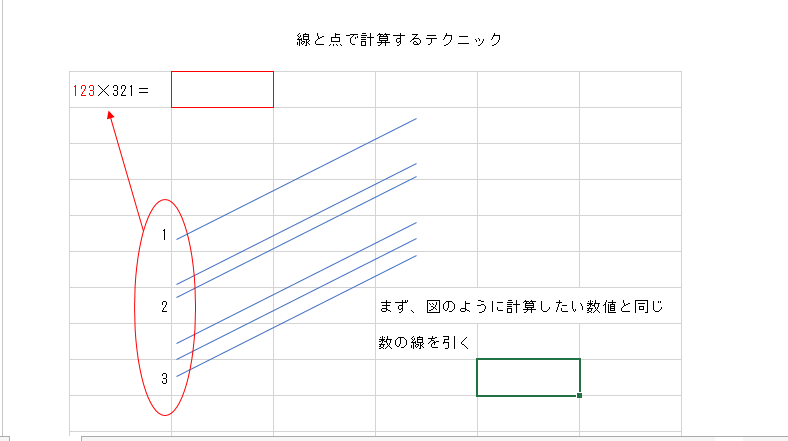
-
同様に掛ける数字の数に応じて縦線を引く
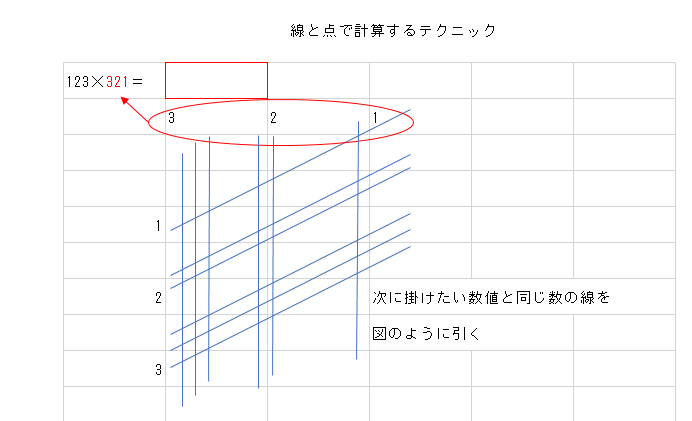
- 順序どおりに点の数を数えていく
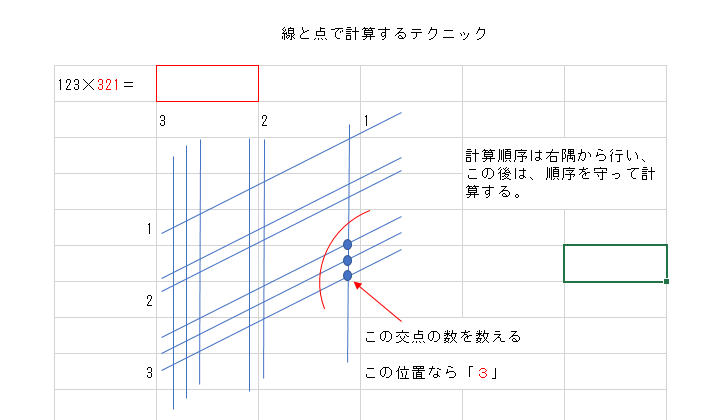
ここでは交点の数は「3」です。 -
次は縦・横共に1スパン移動して点の数を数える

この時、結構書き込みが多くなると順序を間違える場合があるため、コツとしては下図のように覚えれば簡単。
あくまでも平行四辺形の対角線上を見ることですね。
ここの線上では「8」です。 - 次の線上の交点を数える

ここは「14」ですね。 - 最後の左隅の交点の数を数える
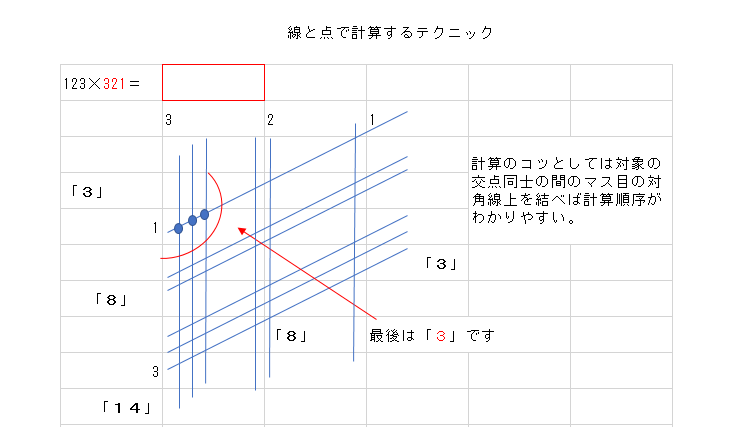
ここでは「3」という数字が出ます。 - 下図の順番で出た交点の下図を並べて行く
ただ並べるだけなら「3」、「8」、「14」、「8」、「3」という羅列になるのですが、そこは算数と一緒で10の位の余分な部分は繰り上げを行わないといけません。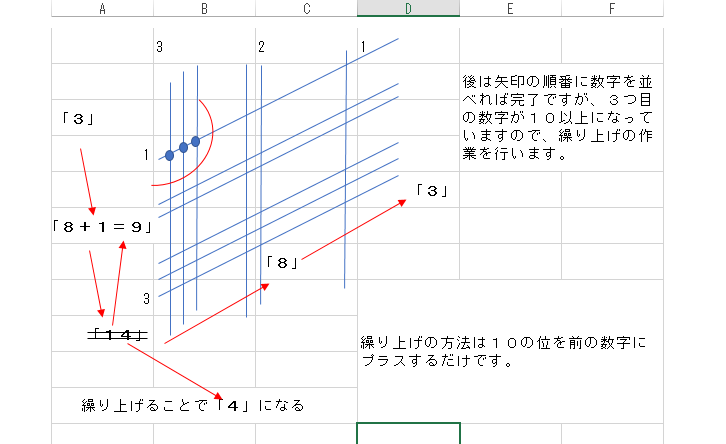
その繰り上げのルールは前の数字に10の位の数字を移動してプラスしてあげるだけです。
上記の数字から考えると3番目の「14」という数字の「1」を直前の「8」に繰り上げて「8+1=9」、「14」という数字は「1」がなくなるので「4」になりますね。 -
もう一度数字を順番通りに並べれば計算完了
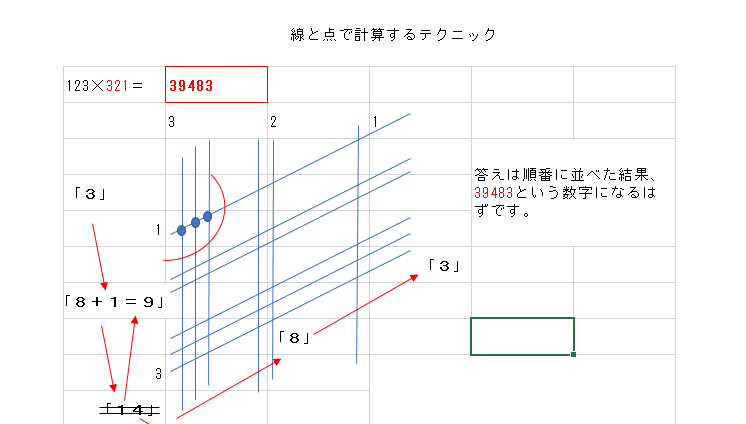
123☓321=39483となります。
一応、電卓も叩いてみましたが間違いないようです。
数字間に0が交じる数字の計算方法
そして、103☓123のように数字の間に「0」が交じる場合もあります。
この時は「0」に対しても線は引きますが、解るように色を変えるなり、線の形を変えるなどして計算しなければなりません。
これまでエクセルを使って図を挿入し説明しましたが、なにせ飽きっぽい正確なので、もう一通りの図を作成するのは面倒です(笑)
よって、以下の動画を参考にしてみてください。
最後に
いかがでしたか?飽きっぽいという部分は大目に見てもらって、この計算方法知っていた方もおられるんでしょうか?
僕は今日、しかもほんの数十分前に知った事です。
二桁同士の計算であれば暗算のほうが早そうですが、3桁以上であれば使えそうな計算方法ですよね。
色々とノートに書き込んでやってみたら、結構便利な方法でした。世の中には色々な計算方法が存在するのですね~
それでは、今回も最後までお読み頂きありがとうございました。
では、(^_^)/~
過去の記事